Nuclear Physics
Stable nuclei, Nomenclature and units
- Atomic scale is 10-10m, nuclear scale is 10-15m. For convenience we use the unit Fermi (fm) = 10-15m = 1 femtometer. Nuclear sizes range from 1 fm to 7 fm. Particle physics usually happens at an even smaller scale « 10-15m.
- A nuclear species or nuclide is denoted by \(^A_ZX_N\). Here, X is the chemical symbol. Z is the atomic number: the number of protons. A is the mass number: the integer nearest to the ratio between the nuclear mass and the fundamental mass unit (1/12 th of mass of \(^{12}_6C\)). N = A-Z represents the number of neutrons.
- Before the discovery of neutrons, it was believed that nucleus contains A protons along with A-Z electrons to justify the charge. But it is unsatisfactory because: A force stronger than Coulomb is required between protons and electrons; Confining electrons in 10-14m requires momentum of range 20 MeV/c (acc. to Uncertainty principle), but β rays usually have energies less than 1 MeV; total intrinsic angular momentum (spin) of nuclei (A-Z) would disagree with spin addition of A protons and A-Z electrons; nuclei containing unpaired electrons would be expected to have magnetic dipole moments greater than observed.
- Isotopes: Nuclides with same Z but different N (and A). Like \(^{35}Cl\) and \(^{37}Cl\).
- Radioisotopes/radioactive isotopes: unstable isotopes artificially produced in nuclear reactions.
- Isotones: Nuclides with same N but different Z (so X,A) like \(^2H\) and \(^3He\).
- Isobars: Nuclides with same A like \(^3He\) and \(^3H\).
- The properties of nuclides we measure include: mass, radius, relative abundance (for stable), decay modes and half-lives (for radioactive), reaction modes and cross sections, spin, magnetic dipole and electric quadrupole moments, and excited states.
- Black = stable (radioactive lifetime is huge), Grey = Unstable
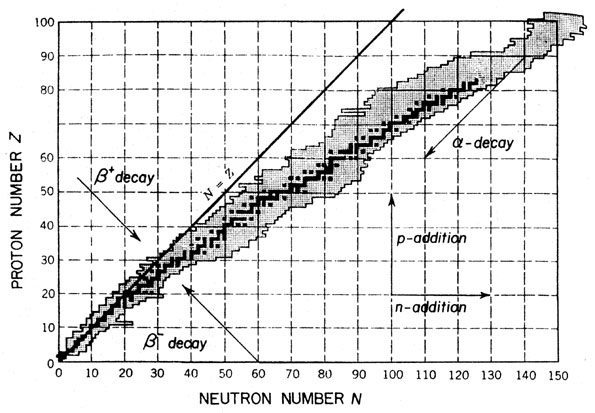
- Typical β and γ decay energies are in the range of 1 MeV, and low-energy nuclear reactions take place with kinetic energies of order 10 MeV which are far smaller than nuclear rest energies. So non-relativistic formulation is justified for nucleons, but β -decay electrons must be treated relativistically.
- Electromagnetic (γ) decays generally occur with lifetimes of order nanoseconds to picoseconds. α and β decays occur with longer lifetimes, often minutes or hours. Many nuclear reactions (\(^5He\) or \(^8Be\) breaking apart) take place in the order of 10-20 s, which is roughly the time that the reacting nuclei are within range of each other’s nuclear force.
Remember
- Z=92 for U, 26 for Fe, 17 for Cl.
- 1 u = 931.502 MeV = 1.661 \(\times 10^{-27}\) Kg.
- 1 eV = \(1.602 \times 10^{-19}\) J: the energy gained by a single unit of electronic charge when accelerated through a potential difference of 1 Volt.
Further Reading
- How does smoke detector’s working depend on nuclear physics.
Size and shape of nuclei
- Like the radius of an atom, the radius of a nucleus is not precisely defined. The density of nucleons and the nuclear potential have similar spatial dependence - relatively constant over short distances beyond which they drop rapidly to zero.
- (Spherical) nuclear shape is characterized by: mean radius, where the density is half its central value, and the skin thickness over which the density drops from near its maximum to near its minimum.
- In some experiments like high-energy electron scattering, muonic X rays, optical and X-ray isotope shifts, and energy differences of mirror nuclei, we measure Coulomb interaction of a charged particle with the nucleus determining the distribution of nuclear charge (primarily distribution of protons but also involving somewhat that of neutrons). In other experiments such as Rutherford scattering, α decay, and pionic X rays, we measure the strong nuclear interaction determining the distribution of nuclear matter.
The Distribution of Nuclear charge
- Shape and size of an object is determined by examining the radiation scattered (elastically) from it for which we need wavelength smaller than the details of the object. For nuclei with diameter 10 fm, we require λ <= 10 fm i.e., p >= 100 MeV/c.
- Rusults for such an experiment looks like diffraction pattern (only an approximation of the potential scattering in 3D) by a circular disk (2D) of diameter D i.e., the first minimum appears at \(\theta = sin^{-1}(1.22 \lamda / D)\).
- Since the nucleus does not have a sharp boundary, the minima do not fall to zero.

Isospin and The Shell Model
- In the absence of magnetic field, there is no distinction between “spin-up” and “spin-down” nucleons.
- The charge independence of strong interaction means that protons and neutrons can be grouped together (as nucleons) analogous to spin: called isospin. In the absence of EM fields, they are indistinguishable.
- The isospin(T) obeys usual rules for angular momentum vectors: length of an isospin vector \(\sqrt{t(t+1}\hbar\); 3-axis projections \(T_3 = m_T \hbar\); and addition rules.
- For any nucleus: \(T_3 = \frac{1}{2}(Z-N)\) expressed in terms of \(\hbar\). T can take any value at least as great as \(\left\| T_3 \right\|\).
Clarifications
- The moodle says 10 best out of 11 assignments. But 8 out of 11 is mentioned in class.
- The ted link on the moodle is not working. What is it supposed to point to?
size and shape of nuclei. Krane: Section 3.1
Lecture 3 (2/8/18): mass, abundance and binding energy of nuclei. Krane: Sections 3.2 and 3.3
Lecture 4 (7/8/18): semi-empirical mass formula. Krane 3.3.
Lecture 5 (9/8/18): spin, parity and magnetic moments. Krane 3.4, 3.5 and 16.1
Lecture 6 (13/8/18) [Wednesday timetable so class at 9am]: the deuteron. Krane 4.1 and 3.5.
Lecture 7 (14/8/18) : cross sections and charge independence. Krane 4.4 and 11.4, Perkins 2.10 and Martin and Shaw, Particle Physics (Wiley), Appendix B.
Lecture 8 (16/8/18): exchange nature of the nuclear force. Krane 4.5, Perkins 2.2.
Lecture 9 (20/8/18) [11am Monday to make-up for cancelled class]: isospin Krane 11.3, Perkins 13.12 and 3.13. The shell model evidence Krane 5.1
Lecture 10 (21/8/18): Basic principles, spin-orbit and shell model predictions; gamma decay Krane 5.1, 10.1-10.4.
[No classes on 22/8 and 23/8]
Lecture 11 (28/8/18): decays in general and resonances. Krane 6.1-6.3, Perkins 2.11
Lecture 12 (29/8/18): alpha decay. Krane Chapter 8.1-8.5
Lecture 13 (30/8/18): beta decay. Krane Chapter 9.1-9.5
Lecture 14 (4/9/18): fission and fusion. Krane Chapters 13 and 14